ASYMMETRICAL CRYPTOGRAPHY - AN OVERVIEW OF DH, RSA AND ECC
2021-07-01
Introduction To Public Key Cryptography
Public key cryptography(also known as asymmetrical cryptography) is a type of cryptography that relies on a pair of cryptographic keys(i.e., private key and public key); this kind of cryptography is the opposed of the symmetrical cryptography where each actor must know the cryptography key before receiving or sending a message.
Introduction To Public Key Cryptography
Asymmetrical cryptography is probably the most important kind of cryptography - at least in computer science - since it allows two parts who have never met each other before to safely exchange information over an insecure communication channel. For instance, TLS relies on this technology to establish secure connections between browsers and servers.
How Does Public Key Cryptography Work?
As we stated before, asymmetrical cryptography relies on a pair of keys: public key and private key. The first one may be distributed to others while the second one must remain secret. These keys are generated in such a way that messages encrypted with the public key, it can only be decrypted with the associated private key. The following diagram should explain this concept: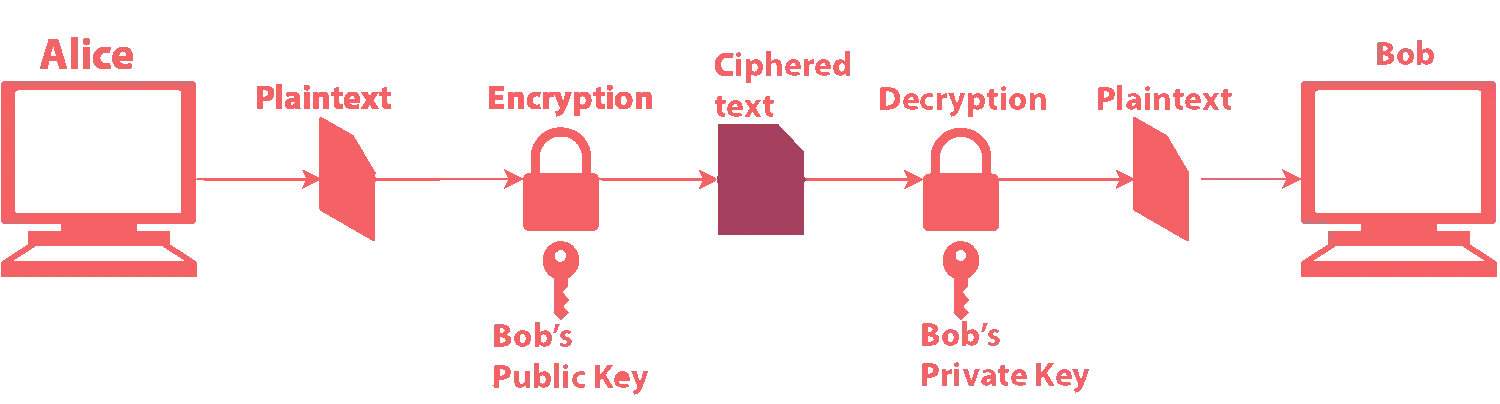
In order to respond, Bob takes Alice's public key and repeat
the same process. This scheme is at the core of the majority of public key
cryptographic protocols; in this guide we will see some of them in details,
explaining their features, advantages and disadvantages, mathematical background and major use cases.
Asymmetrical Cryptographic Algorithms
Here a list of asymmetric key techniques that we shall see on this guide:
- Diffie-Hellman Key Exchange(DHKE)
- Rivest-Shamir-Adleman(RSA)
- Elliptic-curve Cryptography(ECC)
Diffie-Hellman Key Exchange
DHKE is a key exchange protocol that allows two parties to exchange cryptographic keys over an insecure communication channel. DHKE was one of the first public-key algorithm and while it may not be the best solution for today's applicationss, it is the perfect starting point to understand asymmetrical cryptography.
As stated before, DH is not a key-based encryption algorithm; it just allows two computers to exchange a key(using asymmetric cryptography) that will be used later to encrypt data using symmetric cryptography.
The Algorithm
Let us now see the various steps of the DH algorithm. As always, we suppose te two parties involved in the communication are
Bob and
Alice:
- Both alice and Bob, publicly agree to use a prime number p(modulus) and a primitive-modulo-p g(generator);
- Alice chooses a secret number and sends Bob the result of \(A = g^a \ mod \ p\)
- Bob chooses a secret number and sends Alice the result of \( B = g^b \ mod \ p \)
- Alice computes \( s = B^a \ mod \ p \), which is her secret key;
- Bob computes \( s = A^b \ mod \ p \), which is his secret key.
Mathematical background
The whole algorithm relies on two concepts of abstract algebra: cyclic groups and modular exponentiation.
Thus, when both Alice and Bob agree on a prime number p and a generator g, they are in fact agreeing on a finite cyclic group G of order n and a generating element \( g \in G \). The second concept involved in this algorithm is known as modular exponentiation:>A cyclic group \( G \) is an Abelian group that can be generated by a single element \( g \in G \). In other words: $$ G = {g^n \ : \ n \in \mathbb{Z} } $$
To compute such modular exponent we can just compute the exponent directly and then, take the result “modulo-n”.>Modular exponentiation is a type of exponentiation performed over a modulus, in other words: $$ c = b^e\pmod n $$
While this method might be quite simple to understand, it is not the fastest. In fact, there are other algorithms to compute modular exponentiation in smaller order of growth. We shall see just one of them.
Exponentiation by squaring
This method to compute modular exponentiation is a slightly different implementation of a mathematical technique called exponentiation by squaring. The algorithm requires to represent exponent e in base-2: $$ e = \sum_{i=0}^{n-1} a_i 2^i $$ Therefore we can write the exponentiation as: $$ b^e = b^{\left( \sum_{i=0}^{n-1} a_i 2^i \right)} = \prod_{i=0}^{n-1}b^{a_i 2^i} $$ Thus, the solution c is equal to $$ c \equiv \prod_{i=0}^{n-1} b^{a_1 2^i} \pmod n $$ Here a basic implementation in Python:
def mod_pow(b, e, m):
if m == 1:
return 0
else:
r = 1
b = (b % m)
while e > 0:
if (e % 2) == 1:
r = (r*b) % m
e = e >> 1
b = (b^2) % m
return r
The algorithm has a running time of \( \mathcal{O}(\log e) \), meaning that if the exponent
was \( 2^{50} \) then \( 2^{50} \in \mathcal{O}(\log 50) \).
Finally, let's see a worked example:
- Alice and Bob agree to use \( p = 17 \) and \( g = 3 \) (the first one is a prime number, while the second one is a primitive root modulo 17);
- Alice chooses \( a = 5 \) as a private number and sends Bob the result of \( A = 3^5 \pmod{17} = 5 \);
- Bob chooses \( b = 4 \) as a private number and sends Alice the result of \( B = 3^4 \pmod{17} = 13 \);
- Alice retrieve the shared password with \( s = 13^5 \pmod{17} = \boxed{13} \);
- Bob retrieve the shared password with \( s = 5^4 \pmod{17} = \boxed{13} \)
Advantages And Disadvantages
The main advantage of this protocol is that both parties involved in the data exchange do not have to know each other before establishing a connection. The biggest disadvantage of DH is that it does not authenticate any party involved in the communication, this could result in a Man-In-The-Middle attack(MITM) since without any data validation, packets can be easily hijacked and spoofed.
Applications
DHKE is still used today for a wide range of applications. For instance, you can find an implementation of DH on SSH and on the TLS protocol; however when using this protocol without elliptic curves(more on that later), we need to set parameter at 2048 bits(at least).
RSA Cryptosystem
The RSA(Rivest Shamir Adleman) cryptosystem is a public-key algorithm that is used for secure data transmission. The idea behind RSA is the same of Diffie-Hellman key exchange but, unlike this last one, RSA allows us to encrypt/decrypt data asymmetrically(while DH use asymmetrical cryptography just for key exchange) using a pair of cryptography keys.
The safety of this algorithm relies on the difficulty of factoring a product of two large prime numbers(an NP problem). Since this task would require a ridiculous amount of time, it is literally impossible to break RSA when large prime factors are being involved.
The Algorithm
Before actually encrypting the data we want to transmit, we need to generate a pair of cryptographic keys and distribute the public one. Let us get started by analyzing the key generation process:
- Choose two random prime numbers \( p \) and \( g \). These two numbers must remain private;
- Compute \( n = p \cdot q \), it will be used as the modulus for other computation. Also, do note that their product \( n = p \cdot q \) should be equal to the required bit length(for instance, 1024);
- Use Euler's totient function to compute \( \phi = (p-1)(q-1) \);
- Choose an integer \( 1 < e < \phi \) such that \( \gcd(e, \phi) = 1 \)(i.e., they are coprime);
- Compute the exponent \( 1 < d < \phi \), such that \( ed \equiv 1 \pmod{\phi(n)} \)
- The public key \( (n,e) \);
- The private key \( (n,d) \);
- p, g and \( \phi \) must also remain secret, since they could be used to determine d. In fact, you can discard all of them after has been successfully generated.
We are now ready to send encrypted data! Before anything else, the sender must convert its plaintext into an integer m(such that \( 1 < m < n \)) using a pre-agreed padding scheme. Then, we can use receiver's public key \( (n, d) \) to compute the ciphered text: $$ c = m^e \pmod n $$ The number c can now safely send to the receiver. After receiving the ciphered text c, the recipient extract the original padded plaintext m using its private key \( (n,e) \): $$ m = c^d \pmod n $$ Finally, the recipient reverse the padding scheme to recover the plaintext message.
Mathematical proof using Fermat's Little Theorem
To prove the correctness of the RSA algorithm we need to make a step back understand the math behind it. In fact, RSA algorithm can be proven using Fermat's Little Theorem.
Fermat's Little Theorem
To avoid confusion about this theorem(since there are two other theorems with the same name), let's quickly recall its statement:
In other words, this theorem states that if we take any integer, we multiply it by itself p times, and then we subtract a, the result is a multiple of p . We will omit the proof of this theorem since it is behind the scope of this guide, but you are encouraged to read it by yourself.>Let \( p \) be a prime number and let \( a \) be an integer \( a \in \mathbb{Z} \) then: $$ a^p \equiv a \pmod p $$ Furthermore, if \( \gcd(p,a) = 1 \) then $$ a^{p-1} \equiv 1 \pmod p $$
RSA Proof
We now have all the resources needed to prove RSA! As we saw above, Fermat's Little Theorem states that \( a^{p-1} \equiv 1 \pmod p \) for any integer \( a \) and a prime p not dividing \( a \). We want to do the same thing but using the following notation: $$ (m^e)^d \equiv \pmod{n} $$ Where \( n = p \cdot q \) Since \( ed \equiv 1 \pmod{\phi(n)} \) we have \( (m^e)^d = (m^k)^{\phi(n)+1} \). We also know that \( \phi(n) = (p-1) (q-1) \) and this implies that \( \phi(n) \) is a multiple of \( p - 1 \). Thus, \( k \phi(n) \) is also a multiple of \( (p-1) \). Now, due to the fact that \( p \) is a prime number, we can apply Fermat's little theorem: $$ (m)^{k \phi(n)+1} = (m)^1 \pmod p $$ We can do the same thing for the q parameter: $$ (m)^{k \phi(n) +1} = (m)^1 \pmod q $$ In other words, this means that $$ p \mid \left((m)^{k \phi(n) + 1} - (m)\right) $$ and that $$ q \mid \left((m)^{k \phi(n) + 1} - (m)\right) $$ But since both \( p \) and \( q \) are prime and not equal, they are relatively prime, meaning that, for \( a \) and \( b \) relatively prime \( a \mid c \wedge b \mid c \implies ab \mid c \). Thus, we get $$ pq \mid \left((m)^{k \phi(n) + 1} - (m)\right) $$ Which can be rewritten as $$ (m)^{k \phi(n) +1} - (m)^1 \equiv 0 \pmod {pq} $$ $$ \therefore (m)^{ed} \equiv (m)^{k \phi(n) +1} \equiv (m) \pmod n $$
A Worked Example
let's conclude this part of the tutorial by showing a worked example.
Alice:
- She chooses two prime numbers \( p = 11 \) and \( q=23 \), then she computes \( n = 11 \cdot 23 = 253 \);
- Alice computes \( \phi(n) \) which is quite simple since she already knows the factors of \( n \): $$ \phi(253) = (11-1)\cdot(23-1) = 220 $$
- Alice computes the second part of the public key(i.e., e) such that $$ \gcd(e, \phi(n)) = 1 $$ She sets \( e = 3 \);
- Alice computes the second part of the private key(i.e., d) such that $$ ed \equiv 1 \pmod{\phi(n)} $$ Thus $$ 3d \equiv 1 \pmod{220} \implies d = 147 $$
- He encrypts the secret message \( m = 6 \) using $$ c = m^e \pmod n $$ $$ \iff 6^3 \pmod{253} = 216 $$
- He sends the cyphered text \( c = 216 \);
- She decrypts the message using $$ m = c^d \pmod n $$ $$ \iff 216^{147} \pmod{253} = 6 $$
- She reads the secret message \( m = 6 \).
Elliptic-Curve Cryptography
Elliptic-Curve cryptography(ECC) is an alternative technique to RSA that allows to implement public key cryptography. ECC relies on the algebraic structure of elliptic curves over galois field. The benefit of using ECC over RSA is that it generates smaller cryptographic keys while maintaining the same security.
| RSA Key Size | ECC Key Size |
|---|---|
| 1024 | 160 |
| 2048 | 224 |
| 3072 | 256 |
| 7680 | 384 |
| 15360 | 521 |
Galois Fields
Let us introduce the notion of fields in mathematics:
An example of a field is the set of real numbers \( \mathbb{R} \) with the operation of addition and multiplication. At this point we are ready to define Galois fields:>Any non-empty set \( K \) together with two binary operations called addition and multiplication is a field if and only if
- \( (K, +) \) is an Abelian group wit 0 as the neutral element;
- \( (K - 0, * ) \) is an Abelian group with 1 as the neutral element;
- Multiplication is distributive to addition (i.e., \( a(b+c) = (ab) + (ac) \))
This mean that there is a finite field \( \mathbb{F}_{3^2} = \mathbb{F}_9 \) with 9 elements but there is no finite field with 6 elements since the number 6 is not the power of any prime number.>A Galois field(or finite field) is any field with a discrete number of elements with the following properties:
- A finite field has \( p^n \) elements, where \( p \in \mathbb{P} \) is a prime number and \( n \in \mathbb{N} \);
- \( \forall n \in \mathbb{N}, n \geq 1 \) and \( \forall p \in \mathbb{P} \) \( \exists! \ \mathbb{F}_{p^n} \) with \( p^n \) elements, exception made for isomorphism.
Elliptic Curves
In the previous section we defined a particular kind of algebraic field called finite field. This kind of structure are the mathematical environment where elliptic curves lives. In this section we shall see what an elliptic curve is and how does it work.
>An elliptic curve is a plane curve defined over a Galois field given by an equation of the form $$ y^2 = x^3 + ax +b $$ Where the polynomial \( x^3 + ax + b \) must have distinct solutions. In other words the discriminant \( \Delta = 4a^3 + 27b^2 \) must not be equal to zero.
As you can see from the graphs above(source: Wikipedia),
elliptic curves are quite easy to represent and to recognize.
In the following examples,
we will focus on the second kind of elliptic curve since it is a little easier to work with.
Trapdoor Function
A trapdoor function is particular one-way mathematical function that it is easy to compute in one direction but very difficult to compute in the opposite direction. This kind of functions are widely used on cryptography since, unless certain kind of information are known, they are virtually impossible to reverse.
In the context of ECC, the trapdoor function consist in the following steps:
- Choose a point on the curve, let us call it \( A \);
- Choose another arbitrary point \( B \) on the curve;
- Draw a line that intersect both \( A \) \( B \);
- The line should intersect a third point;
- Find the sum of \( A + B \) by reflecting the third point
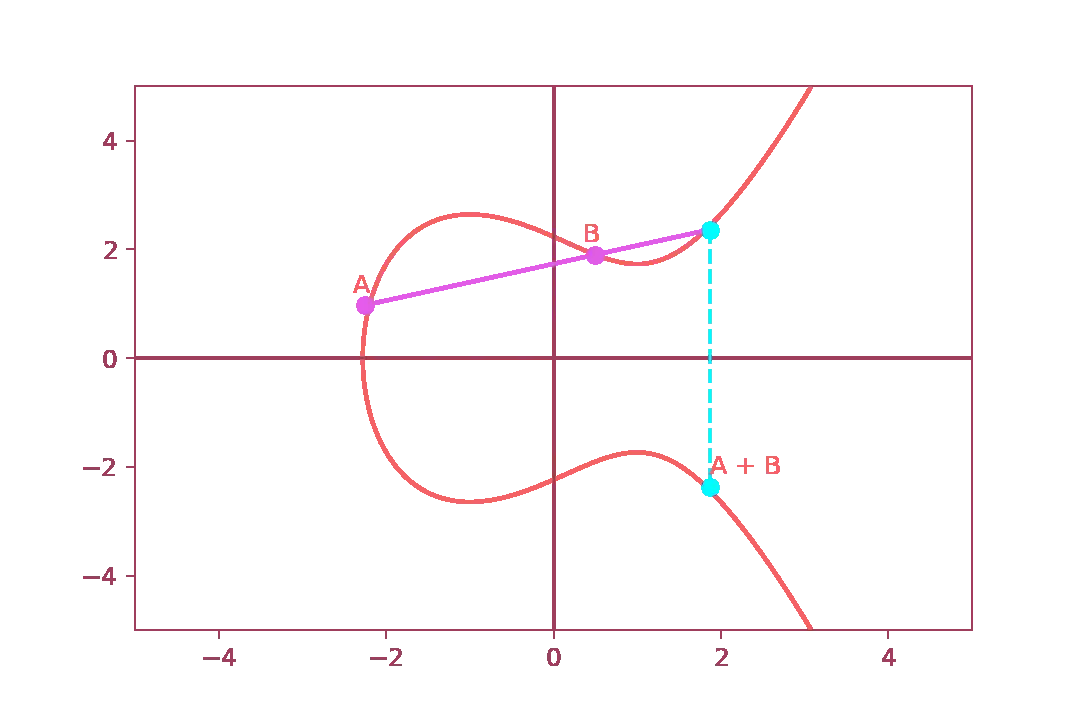And, if we try to repeat this sequence again, we get:
Using this trapdoor function, we can build the public key using the destination point
\( P+Q \) or, more precisely, the coordinates \( (x,y) \)
of the source and of the destination point. Therefore, the private key is just the number
of “hops” needed to arrive at the destination point starting from our initial point \( P \)
Another technique quite similar to point addition is point doubling. In this case we just add the arbitrary point to itself. The procedure consists in the following steps:
- Set an arbitrary point \( P \);
- Draw a tangent line and find a point of intersection on the elliptic curve;
- Reflect the intersection point on the y-axis;
- The result point(let us called it \( R \) ) is the sum of \( P \), meaning \( 2P = P + P \)
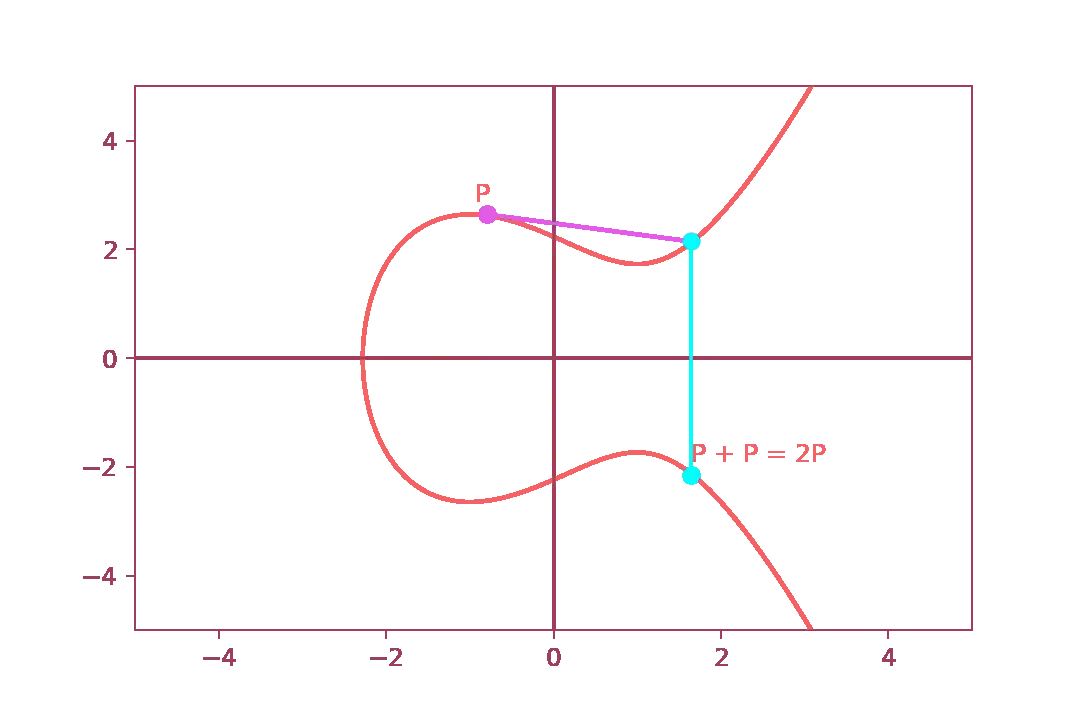Then we repeat the same process to obtain \( 3P \).
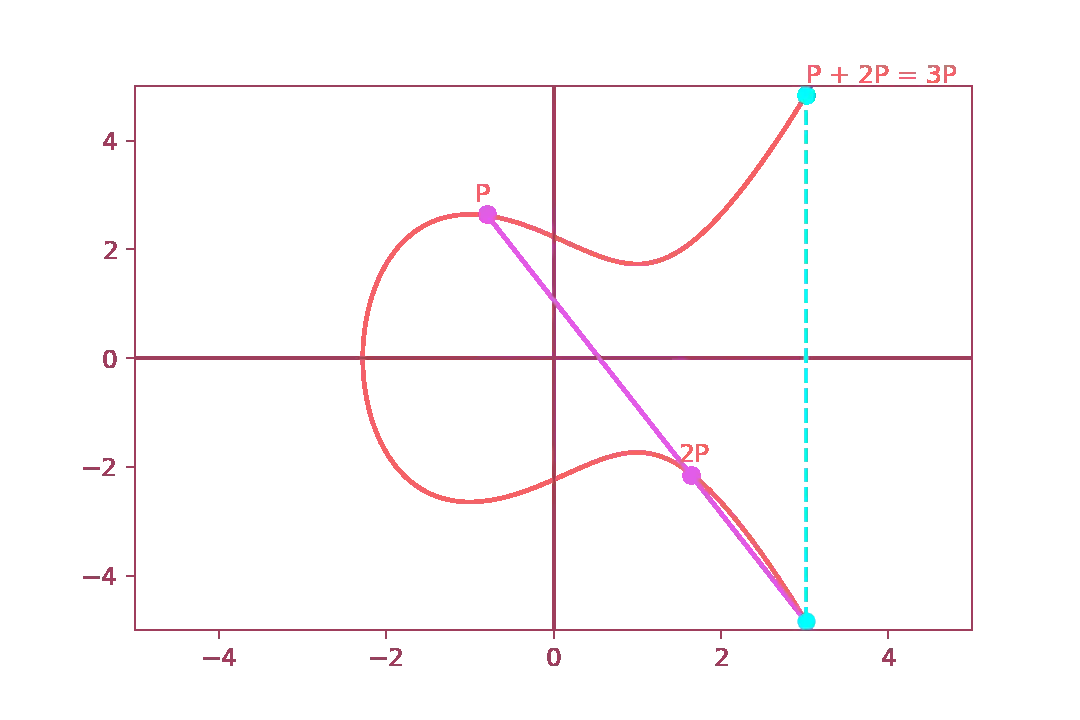Doubling the same point is essentially equivalent to point addition,
but it is easier to repeat and more elegant to implement.
Again, the private key consists in the number of hops \( N \) needed to obtain \( NP \). While the public key consists in the coordinates of the coordinates of the destination point \( NP \). The point \( P \) is a shared value defined by the implementation of the algorithm that both parties involved agree upon communication.
Did I Just Discover A Pitfall Of Elliptic Curves?
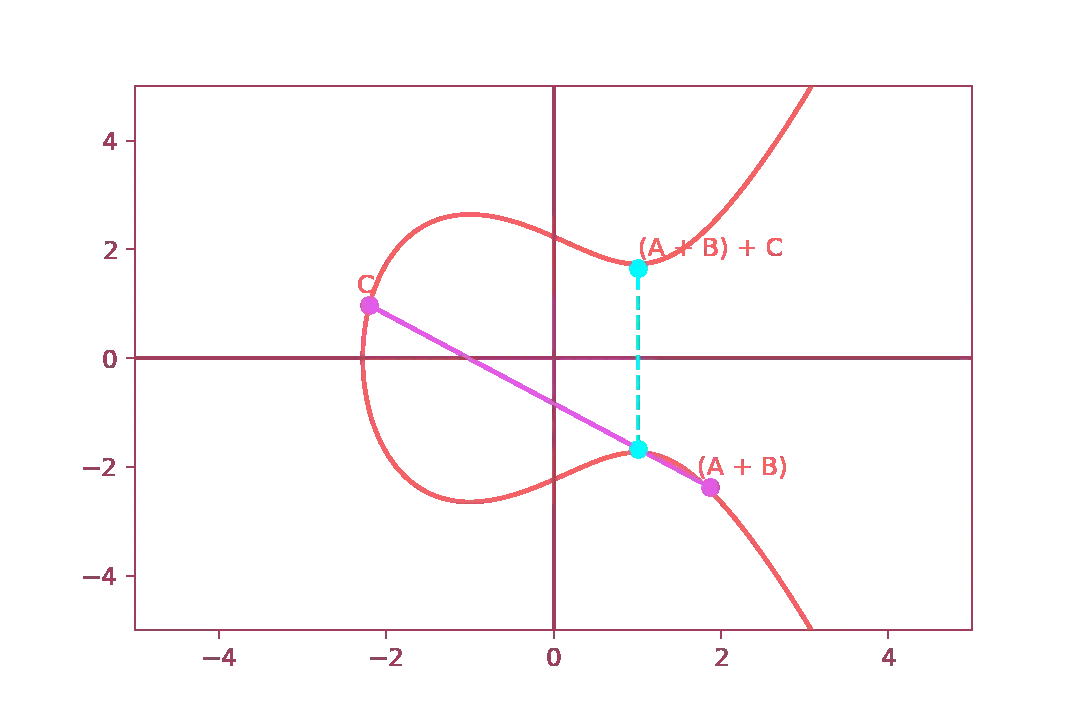
The answer is no. At least not when big values of \( N \) are involved. However, since adding \( P \) to itself \( N \) times is not very fast, we can exploit the algebraic property called associativity. This property tells us the following: $$ (A+B) + C \iff A+(B+C) $$ We will prove this graphically by plotting the result of \( A + (B+C) \), the final point should be equal to \( (A+B)+C \).Q:Can I break the security of elliptic curve cryptography by simply repeating the same process(i.e., multiplying \( P \) to itself \( N \) times) until I get to the coordinates of \( NP \) ?
First, let us add point \( B \) and point \( C \) together:
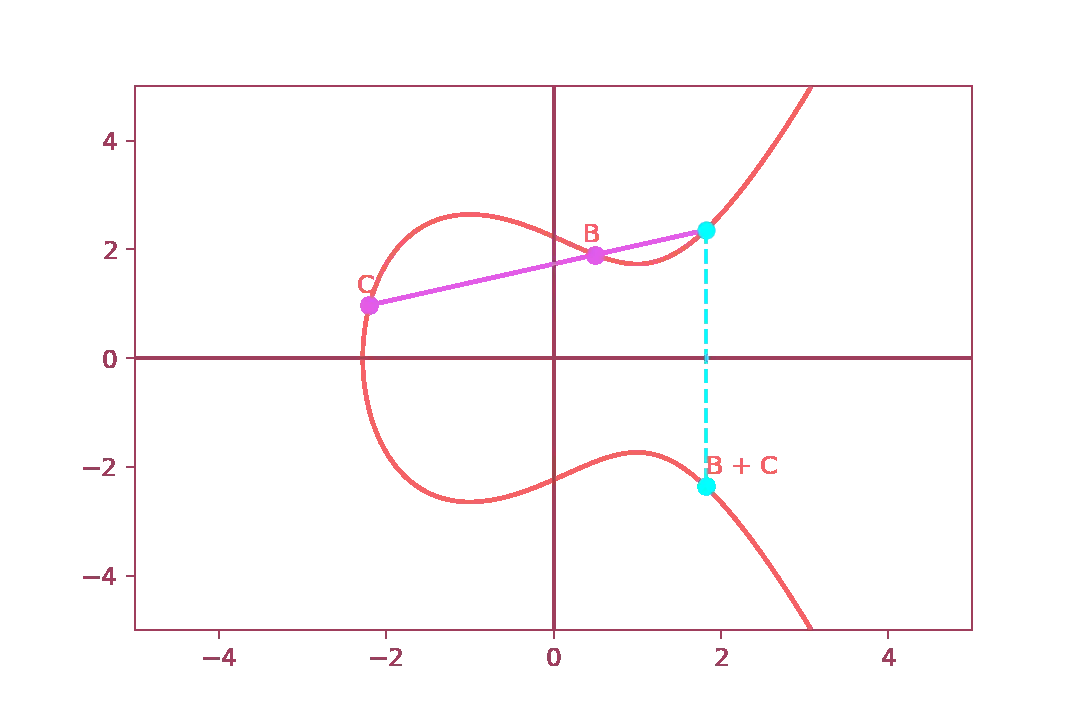Then, let us add point \( A \) and let us find the reflection on the y-axis.
As you can see from the diagram below, the final point is the same as
\( (A+B)+C \):
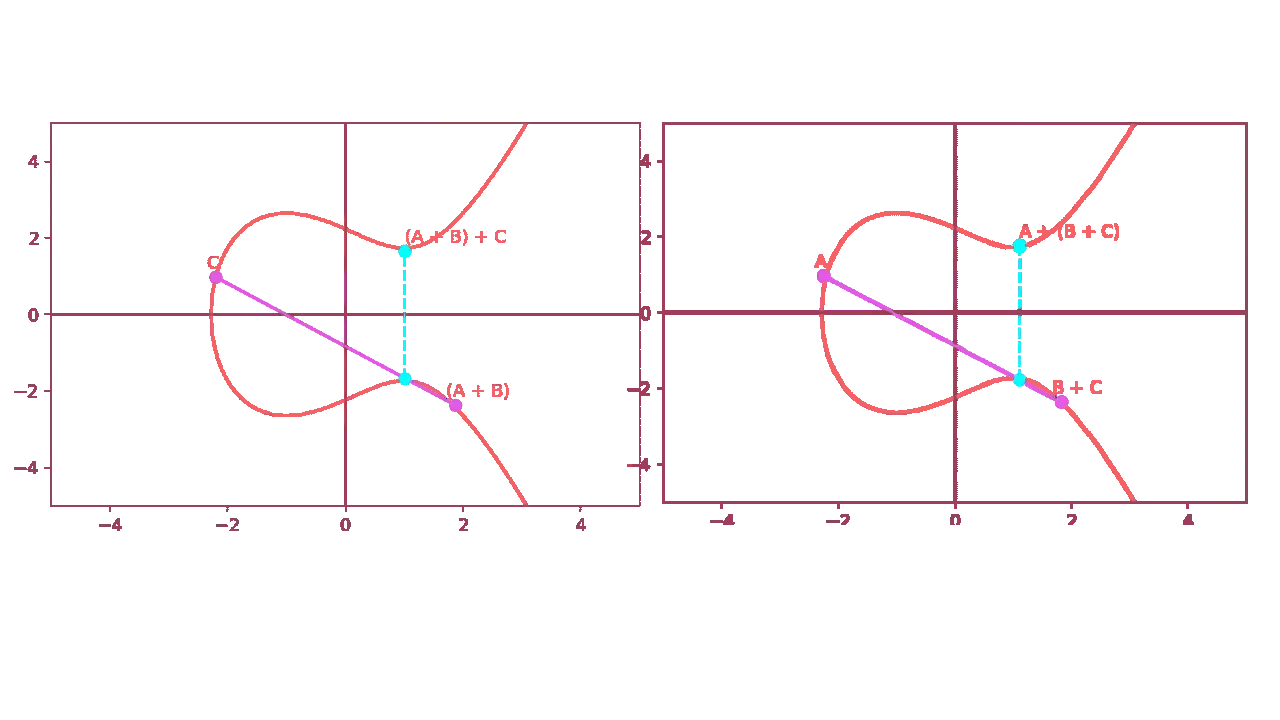If you take a closer look at the two graphs, you will notice that the
final points are not exactly the same. In fact, if you try to repeat this
exact process numerically, you will notice a small distance between the two points.
This is caused by the floating point rounding error and while you may think that is
not very relevant, it is an enormous problem.
We will discuss the issue of ECC with real numbers later.
Let us now go back to our proof and let us prove that $$ P + 3P = 4P $$ it is in fact equal to $$ 2P + 2P = 4P $$ First of all, we compute \( P + 3P \)
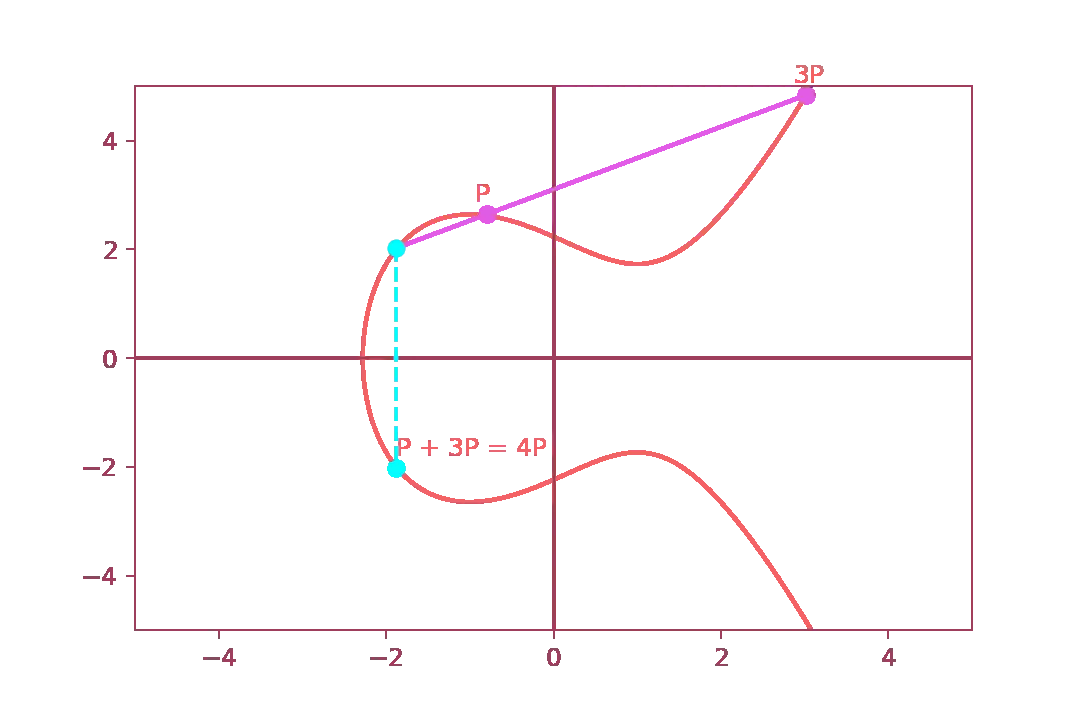And then, we prove that \( 2P + 2P \) is indeed the same
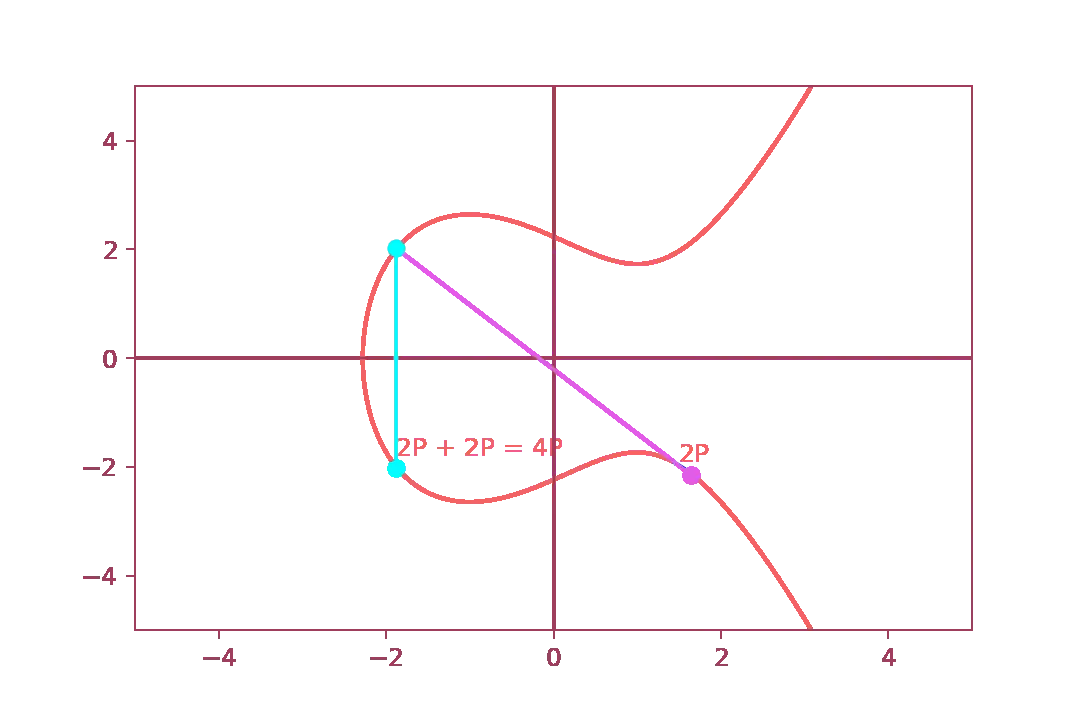This confirms that there are actually two ways to arrive at the same point.
This is great for us since we can continue doubling our point until we obtain
the specific power of the point that allows us to complete the value \( N \).
Basically, we can exploit a group theory trick to generate huge values of
\( N \) very fast while, an attacker, has to manually compute
\( P \cdot P \cdot P \cdots \) until \( NP \).
You now may be wondering how to practically use this trick to arrive to
\( NP \).
Well, there is an algorithm for that, and it is called
double and add;
it works as follows:
Suppose that we want to add \( P \) to itself 120 times, that is \( 120P \). First of all let us convert the value 120 to binary: $$ 120_{10} = 1111000_2 $$ Which is the same of $$ 120P = 2^6P + 2^5P + 2^4P + 2^3P $$ and $$ 120P = 64P + 32P + 16P + 8P $$ That is, each binary digit of 120 is expressed as a power of two. Now where double and add algorithm comes into the scene:
- Take \( P \) and double it, we get \( 2P \) (i.e., \( 2^1 P \));
- Do not add anything since \( 2^1 P \) represent a null bit;
- Double \( 2P \), we get \( 2^2 P \);
- Do not add anything since \( 2^2 P \) represent a null bit;
- Double \( 2P \) , we get \( 2^3 P \);
- Add \( 8P \) to the final result(which was empty);
- Double \( 2^3P \), we get \( 2^4 P \);
- Add \( 2^4P \) to \( 2^3P \), we get \( 2^4P + 2^3P \);
- Double \( 2^4P \), we get \( 2^5 P \);
- Add \( 2^5P \) to the final result, we get \( 2^5P +2^4P + 2^3P \);
- Double \( 2^5P \), we get \( 2^6 P \);
- Add \( 2^6P \) to the final result, we get \( 2^6P + 2^5P +2^4P + 2^3P \);
Elliptic Curves Over \( \mathbb{F}_P \)
When we gave the mathematical definition of an elliptic curve, we said that they are a special kind of curves that live in a special algebraic structure called Galois field. However, what we saw in the previous sections, were just examples of elliptic curves with real numbers. They are indeed easier to explain and to understand, but they come with some major problems. We already saw one of these issue: the floating point rounding error. For this reason, we should see how elliptic curves works on finite fields.
In order to define an elliptic curve in \( \mathbb{F}_P \) we need to rewrite its formula like this: $$ y^2 \equiv x^3 +ax + b \pmod P $$ For example, this is the diagram of \( y^2 = x^3 + 2x + 1 \) and \( P = 58 \);
The interesting part about finite fields is that, thanks to the nature of
modular arithmetics, when a point's intersection overpass one of the boundaries,
it actually “reappears” on the opposite part of the field. Believe it or not,
but with this trick we can avoid all of these problems related
to real number's representation on digital computers(IEEE754 standard).
Elliptic Curves Diffie Hellmans
For now, we saw a lot of theory about elliptic curves, but what about some real-world examples? In this section we will discuss a slightly different version of Diffie Hellman algorithm based on elliptic curves. It works very similar to the DHKE algorithm(i.e., it only regards key exchange but not data encryption).
Let us see the procedure step-by-step:
- Alice generates her key pair using the methods previously described. She ends with \( NP \)(pubkey) and \( N \) (privkey); She sends her public key to Bob;
- Bob does the same and sends his public key \( MP \) to Alice;
- Both of them agree on using \( P \) as the starting point;
- Alice computes the shared secret key by adding \( MP \) to itself \( N \) times, that is $$ \underbrace{MP + MP + \cdots + MP}_{N\ times} = N \cdot MP $$
- Bob computes the shared secret key by adding \( NP \) to itself \( M \) times, that is $$ \underbrace{NP + NP + \cdots + NP}_{M\ times} = M \cdot NP $$
- They both end up with the same value(let us call it \( K \) ) since \( (NM)P = (MN)P \).
As the classic DHKE, this algorithm does not provide signature of the keys, meaning that ECDH is vulnerable to MITM attacks.
Discrete Logarithm Problem
In this guide we saw three different algorithms/techniques to encrypt/exchange cryptographic keys using public keys approach. While they are quite different one from another, they all have something in common: the discrete logarithm problem. This mathematical problem is the reason why encryption algorithms that relies on public keys are considered secure. So let us end this guide by giving a quick overview about it.
The “problem” with the discrete logarithm is that is quite easy to compute the exponent of two numbers(we saw the exponentiation by squaring algorithm in the Diffie-Hellman section) but is extremely difficult to compute the inverse in polynomial time. This ensures the security of most of modern cryptography.>Let \( G \) be a finite cyclic group of \( n \) elements. Let \( b \) be a generator of \( G \) , then \( \forall g \in G \) we can use the following notation $$ g = b^k $$ with \( k \in \mathbb{Z} \). We can define the discrete logarithm function as $$ \log_b \colon G \to \mathbb{Z}_n $$ Where \( \mathbb{Z}_p \) is the ring of integers modulo \( n \).
Thus, the function is a group homomorphism.